How To Set An Appropriate Integer Constraint

Excel'southward Solver tool lets y'all solve optimization-modeling problems, besides commonly known as linear programming programs. With an optimization-modeling problem, you desire to optimize an objective function but at the aforementioned fourth dimension recognize that in that location are constraints, or limits. While this abstract definition sounds complicated, at least at the conceptual level, optimization modeling makes common sense once y'all provide a physical example.

EasyRefresher: How Optimization Modeling Works

Suppose, for case, that yous're a residential real estate developer and contractor. You create and sell two products: building lots and houses. Suppose that you brand $20,000 on each dwelling house you build and $xv,000 on each building lot you develop and so sell. Your princi- pal financial objective is to maximize your profits, and this objective tin can exist expressed as an objective function, or equation, that you want to maximize:

$15,000*Lots+$20,000*Houses=Profits

Of course, any objective function is limited by certain constraints. To continue with the fictional example of residential development, suppose that you have 2 principal limiting fac- tors: working capital and bulldozer capacity. Your working capital of $i,200,000 limits the number of lots and houses you can annually sell because every lot requires a $fifty,000 greenbacks investment and every house requires a $25,000 cash investment. The fact that you have a single bulldozer available for simply 3,000 hours each year besides limits the number of lots and houses you can annually sell because every lot requires 80 hours of bulldozing and every house requires 200 hours of bulldozing. These two constraints tin also be expressed as equations. For instance, the working upper-case letter constraint can be expressed as follows:

$50,000*Lots+$25,000*Houses<=$ane,200,000

This formula says the result of the formula $l,000 times the number of lots plus $25,000 times the number of houses must be less than or equal to the working capital limit of $ane,200,000. The less than or equal to symbol is represented by the <= operator.

The bulldozer capacity constraint can be expressed every bit follows:

80*Lots+200*Houses<=3000

This formula says the event of the formula 80 times the number of lots plus 200 times the number of houses must be less than or equal to the bulldozer-hours limit of 3,000. Once more, the less than or equal to symbol is represented by the <= operator.

Typically, you besides accept policy constraints when you work with an optimization-modeling problem. Suppose that as a thing of policy y'all want to maintain a certain level of action both in developing lots and building houses. Yous might say, for example, that because you must maintain your team's expertise in both raw country development and residential contracting that you want to develop at least 10 lots every yr and build at to the lowest degree v houses. These ii constraints as well need to be expressed as equations. The minimum-number-of-lots policy constraint tin exist expressed as follows:

Lots>=10

This formula says that you want to develop at least 10 building lots. Or, restated, this for- mula says that the lots variable must exist greater than or equal to 10. The greater than or equal to symbol is represented past the >= operator.

The minimum-number-of-houses policy constraint can be expressed as follows:

Houses>=five

This formula says that you want to build at least five houses. Or, restated, this formula says that the houses variable must be greater than or equal to ten. Again, the greater than or equal to symbol is represented past the >= operator.

With the data provided in the preceding paragraphs of this EasyRefresherTM, I've described your fictional optimization-modeling problem. You want to maximize your profits, which can be described using the post-obit objective function:

$xv,000*Lots+$xx,000*Houses=Profits

but you can't develop unlimited numbers of edifice lots or build unlimited numbers of houses. Yous are subject to the following constraints:

$l,000*Lots+$25,000*Houses<=$ane,200,000

eighty*Lots+200*Houses<=3000

Lots>=10

Houses>=v

Yous can solve this equation in a variety of ways, including graphically, iteratively, or using a technique like simplex algebra. Or, y'all can provide the objective office and the con- straint equations to Excel and have it solve the problem, which is the solution technique described in the paragraphs that follow.

Solving an Optimization Problem

To use Excel'south Solver, first build a workbook that describes your optimization-modeling problem, including its objective function and any constraints, then tell Solver to look for an optimal solution. As long as you understand the concepts of optimization modeling, as described in the preceding EasyRefresher, this process is simple.

Setting Up Your Workbook for Solver

Y'all take 3 steps to ready upwards a workbook for solver: provide guesses of the variables that optimize your objective part, supply the objective office, and so supply the con- straint functions. Figure 6-17 shows a workbook prepare upwards to solve the case problem dis- cussed in the EasyRefresher.

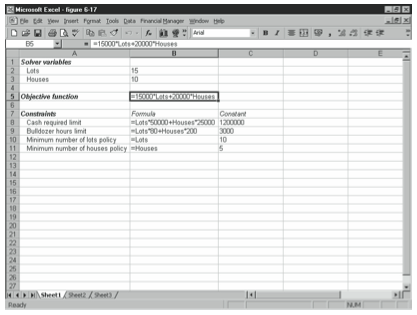
Figure 6-17. A workbook set up for optimization modeling. — Figure half dozen-17. A workbook set up for optimization modeling.

To build this or any optimization model workbook, follow these steps:

Optionally, tell Excel to brandish the bodily formulas rather than results.
ou don't take to have this step, simply because with optimization modeling y'all're really more interested in what the formulas look like as opposed to the results they produce, yous prob- ably want to tell Excel to display formulas rather than formula results. To do this, choose the Tools carte's Options command, click the View tab, and select the Formulas cheque box.
Provide starting guesses for the variables.
You need to provide starting guesses for the variables you lot're trying to optimize. You can practise this simply past entering values in cells, but I recommend you create a pocket-sized schedule of variable names and variable guesses, equally shown in Effigy 6-17 in the worksheet range A1:B3.If you set a worksheet range similar that shown in Figure 6-17—and you really should— yous'll also want to proper noun the cells that hold your guesses. In this case, you can do this by selecting the worksheet range that holds the variable names (Lots, Houses) and guesses— A2:B3 in Figure half dozen-17—and and then by choosing the Insert card's Proper name command and and so choosing the Name submenu's Create command. When Excel displays the Create Names dialog box, select the Left Column check box and click OK.
Describe the objective part.
In Effigy half-dozen-17, the worksheet describes the equation with the post-obit formula located in cell B5:=15000*Lots+20000*HousesBecause the cells belongings the variable guesses have been named Lots and Houses, the objective function uses these names in place of jail cell references. Notation that the label in cell A5 identifies the equation, just you but need to enter the actual equation shown in prison cell B5.
Describe each constraint.
In Effigy 6-17, the constraints are described in the worksheet range B8:C11.To depict a single constraint, yous enter the constraint equation in one cell and the lim- iting constant value in another cell. For example, the working capital constraint men- tioned in the earlier EasyRefresherTM says the formula $50,000 times the number of lots plus $25,000 times the number of houses must be less than or equal to $one,200,000 (the limiting abiding).To draw this first constraint, you enter the following formula in cell B8:=Lots*50000+Houses*25000and you lot enter the abiding value which limits this formula in prison cell C8:
1200000

To describe the 2nd constraint—the one that quantifies the limit on bulldozer capac- ity—you lot enter the post-obit formula in jail cell B9:

=Lots*80+Houses*200

and y'all enter the constant value which limits this formula in cell C9:

3000

To draw the third constraint—which comes from your minimum-number-of-lots policy constraint—you enter the following formula in cell B10:

=Lots

and yous enter the constant value which limits this formula in cell C10:

10

Finally, to depict the fourth constraint—which comes from your minimum-number- of-houses policy constraint—you enter the following formula in cell B11:

=Houses

and you enter the constant value which limits this formula in cell C11:

5

Once you lot've completed the preceding steps, you're ready to use Solver to look for an opti- mal solution to your objective function.

Using Solver

If you set up your workbooks similar to the one shown in Figure 6-17, you will find Solver like shooting fish in a barrel to use. You just follow these steps:

Cull the Tools carte'due south Solver command.
Excel displays the Solver Parameters dialog box (see Figure vi-18).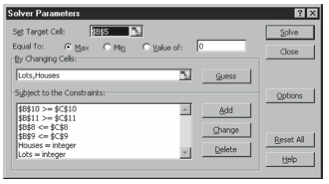

Figure six-18. The Solver Parameters dialog box.
Place the objective function.
Enter the address of the jail cell that holds your objective in the Fix Target Prison cell box. For case, in Figure half dozen-17, jail cell B5 holds the objective role, so yous would enter B5 in the Ready Target Cell box.
Describe how Solver should optimize the objective role.
Utilize the Equal To choice buttons to specify how Solver optimizes the objective function. In the case of a turn a profit function, for example, you lot want to maximize the function and then you click the Max button. This is the case for the workbook shown in Figure 6-17. If your objective function described costs, you would instead want to minimize the office and then would click the Min button. You may besides have situations in which you want to take the objective part return a specific value, and and then in this special case you lot would click the Value Of button and then provide the specified value.
Tell Solver which cells hold your variable guesses.
Use the Past Changing Cells box to tell Excel where y'all've stored the variables used in the objective function and constraint equations. In Figure 6-17, for example, the work- book stores these variables in cells B2 and B3, so you could enter these two cell addresses in the Past Irresolute Cells box. If you've named the variable cells, yous can also type the cell names, as shown in Figure 6-xviii. Cell B2 is named Lots, and cell B3 is named Houses.
Tell Solver yous want to begin describing constraints.
Click the Add button. Excel displays the Add together Constraint dialog box (see Effigy 6-19).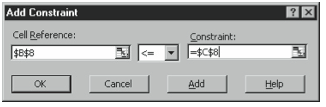

Effigy 6-19. The Add together Constraint dialog box.
Describe the first constraint.
To add a constraint, utilise the Cell Reference box to place the cell holding the kickoff constraint's equation, use the unnamed operator box to select an appropriate constraint operator, and then use the Constraint box to identify the cell holding the kickoff constraint'south constant value. In the instance of the workbook shown in Figure 6-17, for example, you lot might do this by clicking the Cell Reference box and so clicking cell B8, past selecting <= operator, and so past clicking the Constraint box and so clicking cell C8. Figure vi-xix shows how the Add Constraint dialog box should wait to specify this constraint. Click Add to add the constraint. Then repeat this task to add more constraints.
Add whatsoever implicit integer constraints.
In many optimization-modeling problems, you'll as well have implicit integer constraints. What this ways, for example, is that you can't utilise decimal values equally role of the optimal solution. For case, yous might say that y'all must develop an integer number of building lots or build an integer number of houses. Or restated slightly, yous might say that yous tin't get to the finish of the yr and have one of your building lots only half-done or one of your houses only partially complete. To specify an integer constraint, use the Cell Reference box to identify the variable cell that must be integer and then select the int operator from the unnamed drop-down list box. Effigy 6-20 shows how the Add Con- straint dialog box looks when yous specify an integer constraint. Note that you lot don't enter the give-and-take integer in the Constraint box. Excel does that.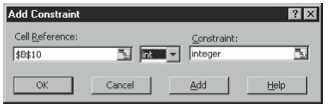

Figure vi-20. The Add Constraint dialog box, this time showing how an integer constraint looks.
Add whatsoever binary constraints.
In a handful of optimization modeling problems, you may also have binary constraints. A binary constraint is i in which the variable must equal either 0 or one. To specify a binary constraint, use the Cell Reference box to identify the variable cell that must exist binary and and then select the bin operator from the unnamed drop-downwards list box.
Tell Excel you're done calculation constraints.
To leave the Add Constraint dialog box later on y'all finish describing your terminal constraint, click OK. Excel closes the Add Constraint dialog box and returns you to the Solver Parameters dialog box. Any constraints you've added show in the Subject To Constraints list box.
Tell Excel to expect for a solution.
Click the Solve push to directly Excel to look for a solution to your optimization-mod- eling trouble. Excel looks for a solution and then displays the Solver Results dialog box (see Effigy half-dozen-21).

Effigy 6-21. The Solver Results dialog box.

This dialog box identifies the variable values that optimize your objective function and asks what yous want to practise with these values.
- To tell Excel to save its solution, click the Continue Solver Solution push and click OK.
- To tell Excel to discard its solution, click the Restore Original Values button and click OK.
- To tell Excel to salvage its solution as a scenario, click the Salvage Scenario button and then provide a scenario proper noun when prompted.

Reviewing Solver Reports

The Solver Results dialog box gives you the option of generating several reports on the optimization modeling that Solver performs. To generate these reports, click the report or reports yous want when Excel displays the Solver Results dialog box (see Figure 6-21).

Understanding the Respond Study

The answer report, which Excel places on a separate worksheet, provides information about how close the optimal solution is to your original guesses and nigh which constraints bind, or limit, optimization. Figure 6-22 shows an example reply written report. At the superlative of the re- port, Excel compares the original objection function formula result with the objection func- tion outcome provided by original variable values. In Figure half-dozen-22, for example, Excel shows the original objective role value as 425000 and the terminal objective part value equally 440000. The Solver in this case improves the objective role by 15000.

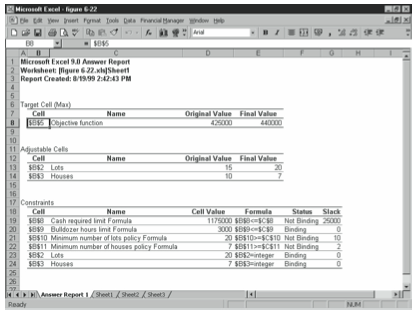
Beneath the comparison of the original and final values of the objective part's formula results, Excel compares the original values and last values of the variables (meet Figure six-22). This information lets you run into exactly by how much Excel adjusts the variables in order to optimize your objective function.

At the bottom of the answer written report, Excel analyzes the constraints past calculating the for- mula results for the constraints then comparison these formula results to the constraint constants. This sounds like busy-work at first blush, but this data is frequently very use- ful in two important means: Get-go, you can use the Status information to run across which constraints are bounden, or limiting. In Effigy 6-22, the binding constraint is the bulldozer hours. Second, y'all tin can use the Slack information to see how close a given constraint comes to becoming binding. In Figure six-22, the working upper-case letter constraint shows only 25000 of slack; in other words, you have just a two% margin of error with your working capital ($25,000 / $1,200,000).

Agreement the Sensitivity Report

The sensitivity report, which Excel also places on a split up worksheet, shows reduced gradients for the variables and the Lagrange multipliers for the constraints (see Figure 6-23). A reduced gradient value shows how the objective function would alter if the vari- able value increased by 1. The Lagrange multiplier shows how the objective function would modify if the constraint abiding increased past 1.

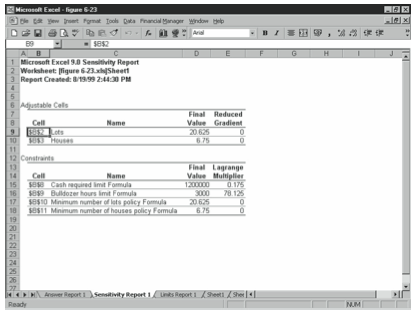
Figure 6-23. The sensitivity report. — Effigy vi-23. The sensitivity report.

A closer inspection of the sensitivity report shown in Figure 6-23, for example, shows that the reduced gradient values for both the Lots and Houses variables equal 0. This indicates that neither value can be increased. The sensitivity written report does show Lagrange multipliers for the working uppercase constraint and for the bulldozer-hours constraint. The Lagrange multiplier for the bulldozer-hours limit, 78.125, indicates that a ane hour increment in the number of balderdash- dozing hours available increases the objective function (your profits) by 78.125.

If you lot've created a linear optimization model—and I'll talk over linear models briefly in the next section, "Customizing Solver's Performance"—your sensitivity reports include several ad- ditional pieces of information, including reduced costs, shadow prices, objective coefficients, and constraint right-hand side ranges.

Agreement the Limits Report

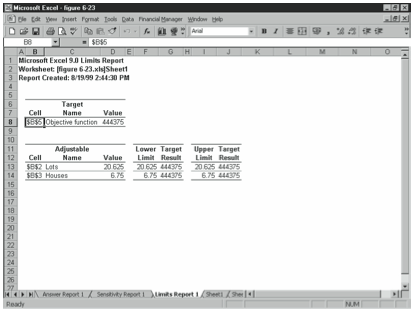
The limits report, which Excel places on withal another worksheet, shows you how much your variable values tin can alter merely still stay within your constraints (run into Figure 6-24). For each variable, the limits report shows the calculated optimal value, the lowest possible value that is allowable, and the highest possible value that is allowable. In Figure 6-24—and this would frequently be the case—the lower limit and upper limit values equal the optimal values. This shows that these variable values tin be inverse without affecting the optimal solution or violat- ing constraints. Note, however, that some optimization problems practice allow you to alter variable values while continuing to optimize the function and continuing to stay within the stated constraints. This happens when there are multiple sets of variable values that opti- mize the equation.

Figure 6-24. The limits report. — Effigy 6-24. The limits study.

Customizing Solver's Operation

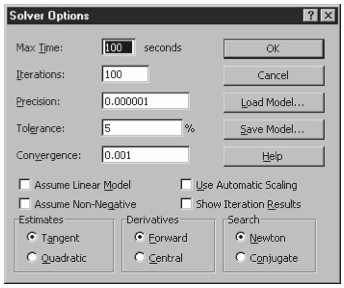
The Solver Parameters dialog box provides an Options button that you can click to display the Solver Options dialog box (see Effigy 6-25). The Solver Options dialog box lets you customize the way in which Solver works out your problem. The paragraphs that follow briefly depict each of the Solver options forth with how and why you might change their settings.

Figure 6-25. The Solver Options dialog box.

Max Time and Iterations

A handful of these options are substantially self-descriptive. The Max Time box, for example, lets you specify how long Solver should work on a problem, and can it exist set every bit high as 32,767 seconds (which is over nine hours). The Iterations box lets you specify how many iterations Solver should work on a trouble, and it tin can exist set as high equally 32,767.

Precision

The Precision box lets you specify how precise Solver should exist in checking a possible optimal solution against your constraints. A precision setting of 0.000001, the default set up- ting, tells Excel that if a constraint formula value is within 0.000001 of the constraint con- stant, it meets the constraint. You can set the Precision box to any value from 0 to 1. To loosen your precision, use a larger Precision value. To tighten your precision, use a smaller Preci- sion value. As you boost your precision, predictably, Excel takes longer to reach a solution.

Tolerance

The Tolerance box lets you lot specify how precise Solver should be in making certain that any integer constraints are met. The default Tolerance setting of v, or five%, means that if an objective function variable is within v% of an integer value—from 95% to 105%, in other words—Excel can consider information technology to be an integer. The Tolerance setting, past the way, applies only to optimization problems that use integer constraints. Equally you lot increase your precision, predictably, Excel takes longer to attain a solution.

Convergence

The Convergence box lets y'all indicate when Excel should end looking for a better solu- tion. You can set the Convergence value to any fractional value betwixt 0 and 1. When the change in the objective function is less than the value shown in the Convergence box, Ex- cel stops looking for a meliorate solution. The Convergence setting, by the way, applies but to nonlinear optimization-modeling problems. As yous reduce the convergence setting (i.e., increase the precision), predictably, Excel takes longer to reach a solution.

Presume Linear Model

If the relationships in your optimization are linear, yous can select the Presume Linear Model bank check box. By doing this, you simplify the calculations that Excel has to brand and, thereby, speed things up.

Assume Non-Negative

If you want to tell Excel that your variables must be equal to or greater than 0 when you oasis't set a lower limit constraint, you can select the Presume Non-Negative bank check box. In effect, when you check this box, you lot tell Excel to create another, implicit set of constraints.

Use Automatic Scaling

Yous should select the Automatic Scaling cheque box when you're working with variables and formula results that differ in magnitude. An example of this situation is when y'all're solv- ing for a rate of return (a percentage) using a set of large dollar variables.

Show Iteration Results

Y'all tin select the Show Iteration Results bank check box to direct Excel to pause after each adding iteration. Subsequently each calculation iteration, Excel displays a Show Trial Solution dialog box. You can relieve the trial solution by clicking the Save Scenario push button. Or you can continue to piece of work toward the solution past clicking the Continue push button. To finish the iterations, click the Terminate button.

Estimates

You use the Estimates option buttons—Tangent and Quadratic—to choose the approach that you desire Excel to use to come up with the first trial solution. Select Tangent if you desire Excel to extrapolate linearly from a tangent vector. Select Quadratic if you want Excel to extrapolate quadraticly—a technique which may yield better results for nonlinear optimization-modeling problems.

Derivatives

You lot use the Derivatives choice buttons—Frontward and Central—to specify the differencing used to approximate partial derivatives of the objective function and constraint function for- mulas. Typically, yous tin click the Forward button. However, if an optimization problem can't be solved with Forward derivatives, y'all tin can click the Primal push button. Using differen- tials virtually the centre of a target often takes more calculations to solve, but tin can be better with highly constrained problems such as airline ticket prices.

Search

The Search option buttons—Newton and Cohabit—permit you cull the algorithm Excel uses to find an optimal solution. If your personal calculator has lots of gratuitous memory, click the Newton push to reduce the number of calculation iterations (albeit at the expense of using more retentivity). If your personal estimator doesn't have extra memory, click the Con- jugate push to permit more than time so that your computer does't use as much memory.

Salve Model and Load Model

The Relieve Model and Load Model buttons let you save an optimization model description. To save a model—such as the equations that you prepare upwards for the scenario with houses, lots, working capital and bulldozers, click the Save Model button and so specify the empty worksheet range that Excel should utilize to salve the model. To load a model, click the Load Model push button so specify the worksheet range holding the model.

Agreement Solver Error Messages

For most simple optimization problems, Excel rather quickly finds a solution to your problem and displays the Solver Results dialog box. In more than complicated problems—unfortunately, those you're likely to encounter in existent life—Excel may run into difficulties. In these cases, information technology may display one of the error messages described in the post-obit paragraphs.

Solver has converged to the current solution

This message ways that while Excel has found what it appears to be a solution, there may be a better solution. To straight Excel to look for a ameliorate solution, reduce the Convergence setting using the Solver Options dialog box, every bit described in the preceding section, "Cus- tomizing Solver'due south Operations."

Solver cannot improve the current solution

This bulletin indicates that Excel has calculated a crude, appropriate solution, but there may be a meliorate solution. To direct Excel to expect for a better solution, accommodate the Precision setting to a larger value using the Solver Options dialog box. Once again, the preceding section explains how to do this.

Stop chosen when the maximum time limit was reached

This message indicates that Excel ran out of time. You tin attempt to retry solving the solutionusingalargerMaxTimesetting.TospecifyalargerMaxTimevalue,usetheSolver Options dialog box.

Stop called when the maximum iteration limit was reached

ThismessageindicatesthatExcelranoutofiterations.Youcanattempttoretrysolvingthe solution using a larger Iterations setting. To specify a larger Iterations value, utilize the Solver Options dialog box.

The Set Target Cell values do not converge

This message indicates that the objective role continues to increment or decrease fifty-fifty though all the constraints are already satisfied. In other words, with each iteration, Excel gets a ameliorate objective function value, but doesn't appear any closer to a final objective function value. If you encounter this error, review your objective function and constraints to brand certain that you lot've correctly described the optimization-modeling problem.

Solver could not notice a feasible solution

This message probably indicates that your optimization-modeling trouble has no answer. Alternatively, this mistake bulletin may propose that you've incorrectly described the objec- tive function or, peradventure more likely, one or more of the constraints. In the previous model, if your working capital was express to $600,000, you would non have enough cash to work the minimum required number of lots and houses. There would be no viable solution.

Conditions for Assume Linear Model are not satisfied

This bulletin indicates you selected the Assume linear model check box, which appears on the Solver Options dialog box, but Excel, after reviewing the calculation results, concludes your model isn't linear. If you see this message, offset display the Solver Options dialog box and select the Use Automatic Scaling check box. Then attempt to solve your optimization model over again. If you get the message error a 2nd time, display the Solver Options box again, but this time clear the Assume Linear Model cheque box. Then endeavor to solve your problem once more.

Solver encountered an error value in a target or constraint prison cell

This message indicates that one of your formulas results in an mistake value or that you've incorrectly specified an integer or binary constraint. To address this Solver problem, you need to prepare the wrong formula.

There is non plenty retention available to solve the problem

This message, as yous would suspect, indicates that Excel doesn't take enough memory to successfully run Solver. To costless up retentiveness, try closing open documents and whatever other open programs. You lot may likewise want to add memory to your personal figurer.